Coefficients de sécurité des voûtes

1  Introduction

La stabilité des voûtes est généralement exprimée à l'aide d'un coefficient de sécurité. Ce dernier permet de mesurer l'écart entre la situation étudiée et la situation critique où la voûte modélisée s'effondre. Il existe plusieurs types de coefficient de sécurité : coefficient de sécurité géométrique, coefficient de rupture, coefficient de sécurité face au glissement etc.

Nous allons passer en revue ces coefficients de sécurité. Nous donnerons à chaque fois des interprétations concrètes de la signification de ces coefficients de sécurité, ainsi que les valeurs pratiques auxquelles doivent être comparées les coefficients de sécurité obtenus par le calcul. Nous présenterons également les coefficients de sécurité partiels $\gamma $ à appliquer aux charges selon les normes actuels, et l'incidence sur les coefficients de sécurité que nous présentons. Nous verrons pour finir deux exemples que les techniques anciennes de calcul de stabilité des arcs peuvent être réinterprétées à partir des coefficients de sécurité utilisé aujourd'hui.

Nous supposerons dans la suite que les bases du calcul à la rupture sont connus par le lecteur, ainsi que les concepts de poussées actives et passives. Nous rappelons simplement que :

• Chaque état d'équilibre d'un arc est représenté par une ligne de pression (line of thrust¹).
• Un état d'équilibre n'est pas nécessairement stable.
• Un état d'équilibre stable est caractérisé par une ligne de pression partout intérieure à la maçonnerie (nous reviendrons en détail sur ce point dans la suite).

2  Coefficient de sécurité géométrique

2.1  Définition

Le coefficient de sécurité géométrique (geometric factor of safety) est noté $\cgs $ dans la suite.

Le coefficient de sécurité géométrique d'un joint soumis à un effort normal de compression $N$ et un moment $M$ est défini comme $\cgs=D\left|\frac{N}{2M}\right|$.

Le coefficient de sécurité géométrique d'une ligne de pression est le minimum des $\cgs $ de l'ensemble de ses joints. Il correspond donc dans le cas d'un arc au rapport entre l'épaisseur de l'arc étudié et l'épaisseur minimale de l'arc contenant la ligne de pression (Fig. 1).

Le coefficient de sécurité géométrique d'un arc est le maximum des $\cgs $ de l'ensemble de ses lignes de pression. Sur la figure 1, la ligne de pression représentée est celle qui correspond au coefficient de sécurité géométrique de l'arc soumis à son poids propre uniquement.

Fig 1: Coefficient de sécurité géométrique D/dd'une ligne de pression

2.2  Interprétation concrète

Ce coefficient de sécurité est simple à interpréter, car sa définition est géométrique, contrairement au coefficient de rupture $F$ que nous verrons plus bas, et qui fait intervenir les contraintes.

Réduction de l'épaisseur de l'arc   Si le coefficient de sécurité géométrique d'une ligne de pression de l'arc vaut...

• 1, cela signifie que cette ligne de pression est exactement contenue dans l'arc, et qu'elle touche l'intrados ou l'extrados en au moins un point.
• 2, cela signifie que cette ligne de pression est contenue dans un arc 2 fois plus fin que l'arc réel.
• 3, cela signifie que cette ligne de pression est contenue dans un arc 3 fois plus fin que l'arc réel. Dans ce cas particulier, on dit que la ligne de pression est contenue dans le tiers-central de l'arc.
• etc.

Si le coefficient de sécurité géométrique d'un arc vaut $x$, cela signifie qu'il existe une ligne de pression qui est comprise dans un arc $x$ fois plus fin que l'arc réel.

Le coefficient de sécurité géométrique d'un joint diverge lorsque la ligne de pression s'approche du centre du joint (division par zéro).

Poussée active et passive   Il est possible d'étendre le concept de poussée active et passive en utilisant le concept de coefficient de sécurité géométrique. Les poussées actives et passives correspondent habituellement à des lignes de pression pour lesquelles le coefficient de sécurité vaut exactement 1. Notons ces poussées $\Hmax(\cgs=1)$ et $\Hmin(\cgs=1)$. Plus généralement nous noterons également $\Hmax(\cgs=x)$ et $\Hmin(\cgs=x)$ les poussées actives et passives correspondant à des lignes de pression de coefficient géométrique de sécurité $\cgs $ égal à $x$. On déduit des propriétés des lignes de pression que :

1. Si le coefficient géométrique de sécurité d'un arc vaut $x$ supérieur à 1, alors $\Hmax(\cgs=x)=\Hmin(\cgs=x)$ et $\Hmax(\cgs=1)>\Hmin(\cgs=1)$.
2. Les poussées actives et passives correspondant à un coefficient de sécurité géométrique plus grand que 1 sont comprises dans l'intervalle défini par $\left[\Hmin(\cgs=1)~;\Hmax(\cgs=1)\right]$.
3. Si le coefficient géométrique de sécurité d'un arc vaut $x$=1 alors la seule poussée admissible pour l'arc est $H=\Hmax(\cgs=1)=\Hmin(\cgs=1)$

Méry résume ces propriétés ainsi :

Entre ces deux extrêmes [poussées minimale et maximale], il se trouve une infinité d'autres courbes qui donneraient pour la poussée des valeurs intermédiaires ; elles n'existent que dans le cas où la voûte a des dimensions plus que suffisantes, et se confondent toutes en une seule, quand l'épaisseur est réduite au minimum exigé pour l'équilibre.

Méry 1840 [7]

Reprenons les exemples que nous avions déjà présenté dans notre article précédent sur les poussées actives et passives. On trouve dans le cas du plein cintre (Fig. 2 et 3) que :

• $\Hmin(\cgs=2,0)=1,39\times\Hmin(\cgs=1,0)$
• $\Hmax(\cgs=2,0)=0,76\times\Hmax(\cgs=1,0)$

Dans le cas de l'arc ogive (Fig. 4 et 5) :

• $\Hmin(\cgs=2,0)=1,36\times\Hmin(\cgs=1,0)$
• $\Hmax(\cgs=2,0)=0,82\times\Hmax(\cgs=1,0)$

Fig 2: Arc plein cintre - poussée passive (g.) et active (d.) - csg = 1,0

Fig 3: Arc plein cintre - poussée passive (g.) et active (d.) - csg = 2,0

Fig 4: Arc ogive - poussée passive (g.) et active (d.) - csg = 1,0

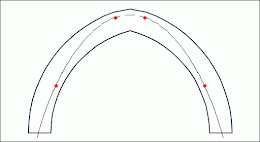
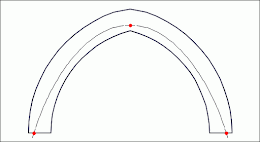
Fig 5: Arc ogive - poussée passive (g.) et active (d.) - csg = 2,0

Fig 6: Arc-boutant A - poussée passive - csg 1,0

Fig 7: Arc-boutant A - poussée passive - csg 2,0

2.3  Valeurs pratiques

Arcs   Dans le cas des arcs, Heyman indique qu'un coefficient de sécurité géométrique de 2,0 semble être suffisant pour assurer la stabilité, et tenir compte des éventuelles asymétries créées par des tassements, ou par les chargements accidentels (Heyman 1995 [4]). Cette valeur de 2,0 est mentionnée par Ochsendorf et al. (2004 [8]). Elle peut également être appliquée aux voûtes en berceau.

Il existe dans la littérature des études de cas réels, où les calculs donnent un coefficient de sécurité inférieur à 2. Huerta et López présentent un tel exemple, qui illustre l'évolution du coefficient de sécurité d'une voûte en berceau suivant les renforts qui sont ajoutés (1997 [6]).

Par ailleurs, si on fait l'hypothèse que les contraintes dans les sections sont linéaires, et que la traction n'est pas admissible, on aboutit au résultat suivant : la résultante des forces doit être contenue dans le tiers central. Cette "règle du tiers central" correspond à imposer un coefficient géométrique de sécurité égal au moins à 3,0 pour considérer que l'arc est stable. Cette règle est aujourd'hui fermement rejetée par de nombreux auteurs (Heyman, Delbecq, Huerta, etc.) pour la vérification des bâtiments existants, car elle est trop conservative.

Voûtes   Dans le cas des voûtes (en dehors du cas évident des voûtes en berceau), il est possible de se ramener à l'étude d'une série d'arcs en découpant la voûte en une série de tranches (slicing technique). .

Il n'existe pas à notre connaissance de publications claires sur le coefficient de sécurité à retenir pour ces arcs issus du découpage des voûtes. Il est possible de prendre la valeur 2,0 comme ci-dessus, mais il existe de nombreux exemples de voûtes stables pour lesquelles il ne semble pas possible de trouver de découpage permettant d'obtenir des coefficients de sécurité géométrique supérieurs ou égal à 2,0. Cela est le cas en particulier pour les voûtains à double courbure, pour lesquels la méthode de découpage en tranche semble trop conservative.

Les dômes forment un cas particulier en raison du développement des forces le long des parallèles. Nous n'aborderons pas le cas des dômes dans cet article.

Piédroits et murs   Dans le cas des piédroits et des murs soumis à une force horizontale, le coefficient de sécurité généralement retenu dans la littérature vaut 3,0. La problématique des piédroits nécessite à elle seule un article entier. A ce sujet, voir l'article de Ochsendorf et al. 2004 [8].

Murs de soutènement   A titre d'information nous signalons que selon Rankine, le coefficient de sécurité des murs de soutènement sans structure en surface peut-être abaissé à 1,5 (rapporté par Oikonomopoulou 2009 [9]).

3  Coefficient de rupture

3.1  Définition

Dans la suite, la compression est comptée positivement (pour $\sigma $ ou $N$).

Delbecq développe en 1983 une nouvelle méthode à partir de l'hypothèse suivante, qui diffère de celle alors habituellement retenue pour l'analyse limite : la maçonnerie à une résistance nulle à la traction et finie à la compression (1983) [2]. \begin{align} 0 \leq \sigma \leq \sigo \end{align}

Cette hypothèse est justifiée par le type de structure étudiée par Delbecq. Il développe dans sa thèse un mode de dimensionnement pour les ponts routiers, ferroviaires, et les tunnels, structures qui sont soumises à des contraintes plus élevées que celles apparaissant dans les voûtes de couvrement de bâtiments. A partir de cette hypothèse, et en considérant uniquement des champs de contraintes constants par morceau sur les sections, ce critère de résistance finie donne une condition nécessaire sur le moment $M$ et l'effort normal $N$ s'appliquant au joint (en notant $h$ la demi-hauteur du joint et $S$ son aire) : \begin{align} \left|M\right| \leq Nh(1-\frac{N}{\sigo S}) \label{eq:critA} \end{align} Cette condition se réécrit : \begin{align} (h-\frac{\left|M\right|}{N})/\frac{Nh}{S\sigo} \geq 1 \label{eq:deflambda} \end{align}

Delbecq pose alors le coefficient de sécurité suivant pour chaque joint : $(h-\frac{\left|M\right|}{N})/\frac{Nh}{S\sigo }$. La condition est donc respectée au niveau d'un joint si son coefficient de sécurité est supérieur à 1.

Le coefficient de sécurité d'une ligne de pression est alors définit comme la valeur minimale des coefficients de sécurité de l'ensemble des joints. Le coefficient de sécurité $F$ de l'ensemble de l'arc, appelé coefficient de rupture, est le maximum des coefficient de sécurité de l'ensemble des lignes de pression.

3.2  Interprétation mathématique

Les efforts $N$ et $M$ au niveau de chaque joint peuvent être placés sur le graphique de la figure 8. La condition est remplie si le point $(N~;M)$ est à l'intérieur de la zone $A$.

Si la résistance de la pierre à la compression $\sigo $ est très grande, la condition $(\ref{eq:critA})$ peut se réécrire sous la forme $(\ref{eq:critB})$. On retrouve alors le domaine de stabilité utilisé par Heyman (1966 [3]). Cette condition est remplie si le point $(N~;M)$ considéré est à l'intérieur de la zone $A$ ou $B$. \begin{align} \left|M\right| \leq Nh \label{eq:critB} \end{align}

Fig 8: Domaine de stabilité

3.3  Interprétation concrète

Mesure de la résistance à la compression   Si le coefficient de rupture d'une ligne de pression est supérieur à 0, alors la ligne de pression est une ligne partout comprise à l'intérieur de la maçonnerie. Cependant, l'utilité de ce critère ne se situé pas là. L'information intéressante est la suivante :

• Si le coefficient de rupture d'une ligne de pression vaut 1, cela signifie que le pic de compression² relatif à cette ligne de pression atteint la valeur de la compression limite de la maçonnerie $\sigo $.
• Si le coefficient de rupture vaut 2, cela signifie que le pic de compression dans l'arc atteint la valeur $\sigo/2$.
• Si le coefficient de rupture vaut 3, cela signifie que le pic de compression dans l'arc atteint la valeur $\sigo/3$.
• etc.

Comparaison au coefficient de sécurité géométrique   Si la résistance de la pierre à la compression $\sigo $ est très grande devant les contraintes mises en jeu dans l'arc, alors :

• Pour une ligne de pression de coefficient géométrique de sécurité=1, le coefficient de rupture vaut 0.
• Pour une ligne de pression de coefficient géométrique de sécurité>1, le coefficient de rupture est infini.
• Pour une ligne de pression de coefficient géométrique de sécurité <1 (i.e. toutes les lignes de pression possibles sortent de la maçonnerie en au moins un point), le coefficient de rupture vaut $-\infty $.

Le coefficient de rupture $F$ donne donc dans ce cas une indication discrète de la stabilité : stable si le coefficient de sécurité est infini, en situation d'équilibre limite si le coefficient de sécurité est nul, instable si le coefficient de sécurité vaut $-\infty $.

Si la résistance de la maçonnerie est très importante par rapport aux contraintes générée par les charges, le coefficient de rupture peut-être trompeur, en apparaissant très élevé, alors qu'en réalité le coefficient de sécurité géométrique est proche de 1, et les rotules prêtes à se former.

Delbecq propose de prendre un coefficient de réduction d'épaisseur compris entre 0,9 et 1,0 de manière à prendre en compte les incertitudes qui peuvent exister sur l'épaisseur réelle de la voûte (Delbecq 1983 [2, p.162]). Lorsqu'elle est appliquée, cette précaution permet partiellement de contourner la limitation du coefficient de rupture mentionnée ci-dessus. Si le coefficient de réduction d'épaisseur vaut 0,9, le coefficient de sécurité géométrique d'une voûte stable selon le coefficient de rupture est au moins égal à 1,11.

Le coefficient de rupture $F$ est donc plus particulièrement adaptée pour la vérification des ponts et des tunnels reprenant des charges importantes.

3.4  Valeurs pratiques

Delbecq indique que le coefficient de rupture $F$ doit être supérieur à 3, si on prend pour $\sigo $ la résistance caractéristique (et non la résistance moyenne) de la maçonnerie $\fk $ (1983 [2, p. 162]).

4  Coefficient de sécurité face au glissement

Les coefficients de sécurité que nous avons vu jusqu'à présent n'expriment pas la sécurité vis-à-vis au glissement. Il est vrai que les glissements se rencontrent assez rarement pour les voûtes sous sollicitations statiques. Cependant, ces glissements peuvent se produire, par exemple en tête des arcs boutants lorsque leur poussée est proche de la poussée passive (voir fig. 6), sur des arcs très massifs (voir par exemple les exemples donnés par Petit 1835 [10]), ou sur des arcs soumis à des chargements dynamiques (Oikonomopoulo 2009 [9, p.130]).

Il est possible de définir un coefficient de sécurité face au glissement, en prenant par exemple le rapport entre l'angle $\phi $ de la résultante des forces par rapport à la normale au joint, et l'angle limite de frottement de la maçonnerie considérée.

Les valeurs limites de l'angle de frottement sont généralement comprises entre 30 et 35^o(Huerta 2001 [5]), mais elles dépendent naturellement de la nature de la maçonnerie. Nous reviendrons de façon plus complète sur ces valeurs limites dans un prochain article.

Etant donné que ce mode de rupture est assez rare, nous n'avons pas trouvé de valeurs pratiques préconisées dans la littérature pour le coefficient de sécurité face au glissement.

5  Normes actuelles

5.1  Etats limites

Les normes actuelles exigent la vérification du dimensionnement des structures par rapport à des états limites. On distingue les états limites ultimes (ELU), qui correspondent à la situation où la sécurité de la structure et des personnes n'est plus assurée, et les états limites de service (ELS), qui correspondent à la situation où la structure ne peut plus être utilisée dans des conditions normales, du point du vue du fonctionnement, du confort des personnes, ou de l'aspect (fissures, flèche etc.).

Les états limites étudiés dans le cadre de l'analyse des voûtes sont les ELU, que l'on découpe en deux groupes : l'ELU EQU qui correspond à la perte d'équilibre de la structure, et l'ELU STR qui correspond au dépassement de la résistance des matériaux. A chacun de ces état correspond des coefficients partiels de sécurité qui sont appliqués sur les charges.

Le coefficient de sécurité géométrique mesure la stabilité de la voûte par rapport à l'état limite ultime EQU. Le coefficient de rupture et le coefficient de sécurité face au glissement mesurent la stabilité de la voûte par rapport à l'état limite ultime STR. Il faut donc, pour vérifier les voûtes dans le cadre normatif des eurocodes, appliquer aux charges des modèles les coefficients partiels de sécurité prévus par la norme. Nous désignerons dans la suite les coefficients partiels de sécurité par $\gamma $ pour éviter la confusion avec les coefficients de sécurité étudiés ci-dessus.

5.2  Pondération des charges

Variabilité   La variabilité du poids volumique de la maçonnerie est généralement élevée. La norme impose de considérer deux valeurs pour ce poids volumique : une valeur inférieure $G_{k,inf}$ et une valeur supérieure $G_{k,sup}$. La valeur inférieure sera utilisée dans les zones où le poids propre a un rôle stabilisateur (par exemple pour les piédroits). La valeur supérieure sera utilisée dans les zones où le poids propre a un rôle déstabilisateur (par exemple les voûtains). En pratique chaque élément peut avoir un rôle stabilisateur ou déstabilisateur suivant les modes de ruines considérés, et il faut donc considérer plusieurs cas de charges. L'étude de cas de Delbecq sur le cas d'une voûte en berceau avec remblai de hauteur variable illustre bien la complexité du choix de ces cas de charges (1983 [2, p.156-158]).

Coefficients partiels de sécurité $\gamma $ sur les charges   Dans le cadre d'une vérification de l'ELU EQU, on multipliera :

• par $\gamma_{Gsup}$=1,1 les charges propres défavorables (pour lesquelles on aura pris $G_{k,sup}$)
• par $\gamma_{Ginf}$=0,9 les charges propres favorables (pour lesquelles on aura pris $G_{k,inf}$)
• par $\gamma_{Q}$=1,5 les surcharges d'exploitation défavorables
• par $\gamma_{Q}$=0 les surcharges d'exploitation favorables

Dans le cadre d'une vérification de l'ELU STR, on multipliera :

• par $\gamma_{Gsup}$=1,35 les charges propres défavorables (pour lesquelles on aura pris $G_{k,sup}$)
• par $\gamma_{Ginf}$=1,0 les charges propres favorables (pour lesquelles on aura pris $G_{k,inf}$)
• par $\gamma_{Q}$=1,5 les surcharges d'exploitation défavorables
• par $\gamma_{Q}$=0 les surcharges d'exploitation favorables

5.3  Coefficients de sécurité

Revenons maintenant aux trois coefficients de sécurité que nous avons défini ci-dessus pour les voûtes. Les valeurs pratiques que nous avons donné pour les coefficients de sécurité dépendent bien évidemment des $\gamma $ qui ont été appliqués aux charges.

Les $\gamma $ appliqués par Delbecq sur les charges sont assez proches de ceux des eurocodes, ce qui permet de réutiliser sans trop de difficulté la valeur pratique de 3 que Delbecq propose. Il faut cependant s'assurer que la définition de la résistance caractéristique de la maçonnerie $\fk $ dont on dispose correspond bien à celle utilisée par Delbecq.

Dans le cas du coefficient de sécurité géométrique $\cgs $, les auteurs ne précisent généralement pas si des coefficients de sécurité doivent être appliqués sur les charges. Cela a peu d'influence si seules des charges propres rentrent en jeu³, mais ce n'est pas le cas dans le cas de surcharges d'exploitation.

Les valeurs pratiques données ci-dessus doivent donc être prises avec précaution lorsqu'elles sont utilisées en combinaison avec les $\gamma $ des eurocodes.

6  Réinterprétation des techniques anciennes

6.1  Méthode de Méry

La méthode de Méry est due à l'ingénieur des Ponts et Chaussées du même nom, qui publie en 1840 un mémoire rédigé dix ans plus tôt sur l'équilibre des voûtes en berceau (Méry 1840 [7]). Méry propose dans ce mémoire une méthode graphique appelée à connaître un grand succès. Nous présentons ci-dessous la version originale de Méry, puis sa modification en ce qu'on appelle aujourd'hui l'épure de Méry.

Nous allons voir que la méthode de Méry, dans sa version originale, donne ce que l'on pourrait appeler aujourd'hui un coefficient de rupture $F_{Mery}$, alors que la version actuelle donne un coefficient de sécurité géométrique $D/d$. L'analyse de l'évolution de cette méthode a fait l'objet d'amples développement par Delbecq (1983 [2])

Epure de Méry   Dans son mémoire, Méry s'intéresse spécifiquement aux voûtes en berceau. Il commence par définir la courbe de pression, que nous appelons désormais ligne de pression. Il indique que cette dernière doit être comprise entre l'intrados et l'extrados de la voûte, et que l'équilibre est impossible si elle en sort. Il ajoute qu'il faut de plus un écart suffisant entre la ligne de pression et le bord de la maçonnerie pour éviter l'écrasement des voussoirs. Il indique également que la résultante des pressions ne doit pas être trop inclinée par rapport à la normale au joint, pour éviter le glissement.

Méry explique que la ligne de pression réelle est indéterminée, mais qu'il suffit en pratique de déterminer les deux lignes des poussées extrémales, celle de poussée minimale et celle de poussée maximale. Il donne la méthode graphique qui permet de tracer la ligne de pression qui passe par un point à la clé, et un point choisit ailleurs sur un des joints de la voûte.

Dans un premier temps, Méry fait d'abord l'hypothèse que les voussoirs de la voûte sont infiniment résistants. Il explique que la ligne de pression correspondant à la poussée minimale ou maximale touchera dans un grand nombre de cas l'intrados et l'extrados en des points situés à la clé et aux naissances de la voûte. Il appelle ces joints joints de rupture. Faire une hypothèse sur la position sur les joints de rupture permet de dessiner à partir des principes précédemment exposés les lignes des pressions correspondantes. Eventuellement, si l'hypothèse est inexacte, cela apparaît sur la ligne de pression obtenue, et il est possible de la redessiner à partir des nouvelles informations obtenues lors du premier dessin. On finit par obtenir par tâtonnement la ligne de pression recherchée. Méry présente de nombreux exemples pour confronter sa méthode à des cas présentés par Audoy (calcul analytique) et Boistard (résultats d'expériences). Les lignes de pression trouvées avec cette méthode correspondent à des lignes de pression de coefficient géométrique de sécurité égal à 1 (ligne de poussée active ou passive).

Dans un second temps, Méry indique qu'il faut en pratique tenir compte de la résistance limitée des voussoirs, et qu'il est donc nécessaire d'adapter la méthode présentée ci-dessus. Pour cela, il définit de nouvelles limites plus restrictives que l'intrados et l'extrados pour assurer la stabilité (voir Fig. 9). Pour tracer ces limites, il indique que l'intervalle compris entre la ligne de pression et le bord extérieur doit être capable de supporter les deux tiers de la résultante s'appliquant sur ce joint, et que la résistance à la compression doit être limité au dixième de sa valeur de rupture.

Delbecq propose l'interprétation mathématique suivante du texte de Méry, que l'on compare facilement à $(\ref{eq:deflambda})$ ci-dessus. \begin{align} (h-\frac{\left|M\right|}{N})/\frac{4Nh}{3S\sigo} \geq 1 \end{align}

On en déduit que le coefficient de rupture correspondant à la méthode de Méry $F_{Mery}$ vaut $\frac{3}{4}F$ calculé avec le calcul à la rupture tel que présenté par Delbecq. La valeur pratique minimale que donne Méry pour $F_{Mery}$ est 10. Il n'est pas possible de comparer directement cette valeur à la valeur limite 3 donnée par Delbecq, car le type de résistance pris pour $\sigo $ et la pondération des charges ne sont pas les mêmes. Cependant on voit ici la grande analogie formelle entre les résultats des deux méthodes.

En pratique, si la première partie de la méthode de Méry est simple et élégante par rapport aux calculs proposés par les autres auteurs à cette époque, la seconde partie de la méthode, la diminution du domaine de stabilité, redevient calculatoire, et est très succinctement décrite dans son mémoire. C'est sans doute pourquoi cette seconde partie va être considérablement simplifiée, comme nous allons le voir.

Fig 9: Réduction du domaine de stabilité
d'après Méry 1840 [7]

scanné par la BNF

Epure de Méry et tiers-central   Il est possible qu'à ce stade de notre explication le lecteur trouve cette présentation de la méthode de Méry étrange et ne correspondant pas à ce qu'il connaît de l'épure de Méry. L'explication est simple. La méthode de Méry connait un grand succès au XIX^e siècle, et est reprise par les cours de construction qui l'adaptent aux théories de l'élasticité qui se répandent avec les calculs liés aux constructions métalliques. Cette adaptation va modifier profondément le sens donné à cette méthode.

Les cours de construction du XIX^e siècle reprennent l'essentiel de la méthode, en changeant un détail d'importance : la position de la résultante des forces sur les joints de rupture. Il est ainsi choisi comme position le tiers-inférieur ou supérieur de l'arc, puis vérifié que la ligne de pression ne sort pas du tiers-central (voir par exemple le cours de Croizette-Desnoyers 1885 [1]). Cette méthode correspond donc à imposer un coefficient de sécurité géométrique supérieur à 3, à comparer à la valeur pratique de 2 retenue aujourd'hui par exemple par Heyman (voir ci-dessus).

Comme le souligne Delbecq, l'interprétation tardive de la méthode de Méry a permis la conception de nouveaux ponts avec succès, mais elle ne doit cependant pas être utilisée pour la vérification de structures existantes, car elle est trop conservative.

Bilan   Méry affirme donc dans son mémoire de 1840 que les voûtes doivent un coefficient de sécurité géométrique au moins égal à 1 pour être stable, et qu'il faut en pratique également vérifier que le coefficient de rupture $F_{Mery}$ est supérieur à 10.

La réinterprétation de la méthode a conduit à une nouvelle approche, dans laquelle il est vérifié que le coefficient de sécurité géométrique soit au moins égal à 3, ce qui semble aujourd'hui trop restrictif pour la vérification des voûtes existantes.

6.2  Tables de Petit

Les tableaux publiés par Petit en 1835 dans son Mémoire sur le calcul des voûtes circulaires [10] permettent le calcul des poussées passives (poussées minimales) des voûtes considérés (voir notre article précédent concernant ces tableaux).

Ces poussées correspondent à un coefficient de sécurité de 1. Elles correspondent donc exactement à la valeur de la poussée lors de la formation des rotules, et n'intègrent pas de coefficient de sécurité.

7  Conclusion

Les coefficients de sécurité peuvent donc être définis de plusieurs façons pour estimer la stabilité des voûtes. Chacun de ces coefficients apporte une information différente sur la stabilité de la voûte étudiée. L'informatique permet aujourd'hui de considérer l'ensemble de ces coefficients de sécurité en quelques clics de souris, et ainsi d'étudier en profondeur la marge de sécurité existante pour la stabilité des voûtes.

La facilité à conduire les calculs ne doit cependant pas faire perdre de vue un principe fondamental : si une voûte a été stable pendant des centaines d'années, il est prouvé que cette voûte est stable si son environnement et ses caractéristiques restent inchangés⁴. Lors de l'apparition de désordres, il faudra bien souvent chercher leur origine ailleurs que dans la stabilité intrinsèque de la voûte. Ces origines peuvent être par exemple :

• modification de l'environnement de la voûte : modification des appuis, décaissement des fondations, altération de la capacité portante du sol, disparition d'éléments de contrebutement ou de reprise des poussées, surcharge sur l'extrados, etc.
• perte de matière : vidage des maçonneries, déjointoiement, etc
• dégradation des caractéristiques mécaniques des matériau constitutifs de la voûte.
• etc.

Les coefficients de sécurité seront généralement utiles non de manière absolue, pour juger de la stabilité ou de l'instabilité, mais de manière relative, pour juger de l'effets des changements opérés sur la voûte sur la stabilité de cette dernière, afin de déterminer ceux qui sont déterminants, et ceux qui n'ont pas d'effet.

Article mis en ligne le : 13/01/2013.

Bibliographie

[1]

P.  CROIZETTE-DESNOYERS : Cours de construction des ponts, vol. 1. Paris, dunod édn, 1885.

[2]

J.  DELBECQ : Analyse de la stabilité des ponts en maçonnerie par la théorie du calcul à la rupture. Thèse de doctorat, Ecole nationale des ponts et chaussées, Paris, 1983.

[3]

J.  HEYMAN : The stone skeleton. International Journal of Solids and Structures, 2(2): 249-256, 1966.

[4]

J.  HEYMAN : The Stone Skeleton: Structural Engineering of Masonry Architecture. Cambridge University Press, 1995.

[5]

S.  HUERTA : Mechanics of masonry vaults: The equilibrium approach. In Proc. 3rd International Seminar in Historical Constructions, Guimarães, 2001.

[6]

S.  HUERTA et G.  LóPEZ : Stability and consolidation of an ashlar barrel vault with great deformations : the church of guimarei. Structural studies, repair and maintenance of historical buildings. Southhampton: Computational Mechanics Publications, p. 587-596, 1997.

[7]

E.  MéRY : Equilibre des voûtes en berceau. Annales des ponts et chaussées, p. 51-70, 1840.

[8]

J.  OCHSENDORF, J. I. HERNANDO et S.  HUERTA : Collapse of masonry buttresses. Journal of architectural engineering, p. 88-97, sept. 2004.

[9]

A.  OIKONOMOPOULOU : Approches numériques pour l'étude du comportement des structures maçonnées anciennes : un outil basé sur le calcul à la rupture et la visualisation graphique. Thèse de doctorat, Université Paris-Est ENSA Paris La Villette, Paris, déc. 2009.

[10]

PETIT : Mémoire sur le calcul des voûtes circulaires. In Mémorial de l'officier du génie, num.  12, p. 73-150. de Fain, Paris, 1835.

---

Notes:

¹ Voir Oikonomopoulo 2009 [9, p.44] pour l'évolution historique de la notion de ligne de pression.

² Le pic de compression mentionné ici est lié au choix des champs de contraintes constants par morceaux utilisés pour la définition du critère.

³ En effet, la multiplication de l'ensemble des charges en jeu par un même facteur multiplicatif ne modifie pas $D/d$. C'est là la traduction du caractère uniquement géométrique de la stabilité telle qu'étudiée par le coefficient de sécurité géométrique.

⁴ A l'exception des cas de séismes, tornades et autres calamités naturelles.