1 Introduction
Les cloches sonnées à la volée exercent des poussées sur les beffrois, et par conséquent sur les tours qui les portent. Lors de l'étude structurelle d'un clocher, une des premières étapes concerne donc l'estimation du poids des cloches et de leurs poussées horizontales et verticales. Pour pouvoir calculer ces valeurs, il faut déterminer les équations du mouvement et les résoudre, ce qui ne pose pas de difficulté particulière comme nous allons le voir. Il faut cependant connaître un certain nombre de paramètres qui décrivent la géométrie de la cloche et de son mouvement. La récolte de ces données peut s'avérer plus délicate, en particulier lorsque les cloches sont déjà existantes, et que la fonderie qui leur a donné naissance a disparu. Le relevé de la géométrie du joug et de la position de l'axe de rotation de la cloche ne pose pas de problème. Les difficultés commencent avec la détermination du poids de la cloche, se poursuivent avec la position de son axe de gravité, et continuent avec l'inertie. Nous proposons ici une méthode pour déterminer ces trois paramètres pour les cloches de forme gothique et comparons les résultats de cette méthode avec les données dont nous disposons (tables de différents fondeurs français). Les parties théoriques de cet article s'appuient principalement sur des sources étrangères : anglaises, espagnoles, allemandes, néerlandaises, belges... La théorie du mouvement des cloches et de leurs poussées est évidemment identique pour les cloches françaises. Cependant les paramètres à prendre en compte pour les calculs ne sont pas les mêmes : les tracés, le type de volée et les angles de volées varient suivant les pays. Cette particularité a bien été prise en compte ci-dessous. Nous nous intéressons spécifiquement dans cet article aux cloches sonnées à la volée que l'on peut trouver en France.2 Anatomie des cloches
2.1 Eléments
Une cloche sonnée à la volée est équipée d'un battant, relié au cerveau de la cloche par une bélière. Les anses permettent de lier solidement le cerveau de la cloche au joug. Les efforts qui permettent de mettre la cloche en mouvement sont appliqués par l'intermédiaire d'une roue manœuvrée aujourd'hui par une chaîne et un moteur, autrefois par une corde ou un balancier activés par les sonneurs. Un lexique complet des différents équipements et parties d'une cloche sonnée à la volée peut être consulté sur le site de la Société Française de Campanologie à l'adresse suivante : campanologie.free.fr.2.2 Tracé et profil
Les cloches coulées en bronze utilisées dans les églises ne sont pas antérieures au VIe siècle en France. Parmi ces cloches, les premières sonnées à la volée dateraient du début du XIIIe siècle. La forme des cloches évolue d'une forme très droite, en "ruche", vers une forme plus évasée, en "pain de sucre". Cette évolution aboutit vers le XIIIe ou XIVe siècle à une forme dite "gothique". Cette forme varie dans des frontières assez étroites entre le XIIIe et XVe siècle (Gonon [13]). La forme "gothique" est fixée définitivement au XVIe et XVIIe siècle avec la diffusion des premiers traités décrivant les méthodes de tracé correspondantes (voir Gouriou [14], Deforge [7], Gnehm et Hoffman [12]). Cette forme est assez proche de celle des cloches actuelles. D'un point de vue structurel, le tracé des cloches gothique produites aujourd'hui en France diffère peu de celui des cloches du XVe siècle (Deforge [7, p.46]). Chaque fondeur ayant mis au point son propre tracé, il existe bien sûr des différences entre chacun de ces tracés. Cependant ces différences jouent principalement sur l'acoustique des cloches. Pour le sujet qui nous intéresse - la poussée d'une cloche de forme gothique - les variations de tracé et leur impact sur ces poussées peuvent être négligés. Nous nous intéresserons dans la suite uniquement aux cloches de forme gothique, d'un diamètre supérieur à 60cm. Pour un type de tracé donné, la géométrie d'une cloche est caractérisé par son épaisseur. Par tradition, cette épaisseur est exprimée par le rapport $\d/\t $ appelé profil, avec $d$ le diamètre de la cloche au niveau de la bouche, et $t$ l'épaisseur de la cloche au niveau de la panse. Le profil peut varier entre 9 et 19 d'après les sources disponibles, les profils les plus courants pour les cloches sonnées à la volée semblent être compris entre 11 et 15. Le profil est souvent désigné par une expression plutôt que par sa valeur numérique. On parle alors de profil ultra-lourd (ou extra-lourd, super-lourd), lourd, moyen, léger, ou encore ultra-léger (ou super-léger). Il ne semble pas exister de consensus pour relier à ces expressions des valeurs numériques bien définie. C'est pourquoi nous utiliserons dans la suite les expressions numériques pour désigner les profils $\d/\t $.Fig 1: Evolution de la forme des cloches
Anses non représentées
Anses non représentées
Fig 2: Cloches en "pain de sucre" (Toscane, Italie)
2.3 Matériau
Le bronze des cloches est un alliage contenant environ 78-80% de cuivre et 20-22% d'étain. Ces proportions peuvent varier, en particulier la proportion d'étain (Rupp [20]). Une partie de l'étain était parfois remplacé par du plomb1, moins coûteux. Pour cette raison, il est difficile d'indiquer un poids volumique fiable pour les cloches anciennes. Nous n'avons pu réunir sur la question que les informations suivantes :- Barré [2] indique dans son Mémento en 1896 que la masse volumique des cloches est 8800kg.m−3 ;
- Rupp [20] utilise une masse volumique de 8400kg.m−3 (étude allemande) ;
- Beconcini et al. [3] utilisent une masse volumique de 8434kg.m−3 (étude italienne).
2.4 Sonorité
Les cloches sont des instruments de musique à part entière. Le son d'une cloche se décompose en plusieurs notes qui forment un accord. En conséquence, le son d'une cloche est intimement lié à son tracé. Nous verrons plus loin que le tracé de l'instrument de musique "cloche" ne peut pas être quelconque, et que cela facilite le calcul de sa masse et de son inertie. Pour plus de détails sur le son des cloches, le lecteur pourra se référer aux articles de Duseigne qui présentent un point complet sur la question, avec des extraits sonores : Le son d'une cloche (1), Le son d'une cloche (2) (Duseigne [10] [11]).3 Equations du mouvement
Dans la suite nous appelons cloche* le système mécanique "cloche + joug". L'équation du mouvement d'une cloche* correspond à celle d'un pendule en oscillation quelconque. Elle constitue un préalable au calcul des poussées, car ces dernières sont exprimées en fonction de $\phi{}(\t)$, le déplacement angulaire de la cloche* par rapport à sa position d'équilibre à un instant $\t $. Les articles de Lemmens et Rijnks [17] et de Beléndez et al. [4] décrivent la résolution de l'équation du mouvement à l'aide des intégrales elliptiques. Nous nous intéressons ici uniquement au mouvement de la cloche* et nous négligeons celui du battant, qui aura un effet négligeable sur les poussées de la cloche*. Si en revanche il était souhaitable d'étudier à la fois le mouvement de la cloche* et celui du battant, par exemple pour étudier la vitesse d'impact du battant, la résolution du problème est différente (voir Meneghetti et Rossi [18]). Le déplacement angulaire de la cloche* $\phi(\t)$ est solution de l'équation suivante : \begin{align} (\Js + m s^{2})\phipp + s m g \sin(\phi) = 0 \label{eq:eqmvt} \end{align} Les variables sont notées différemment suivant les auteurs. Les principales notations sont :| DIN4178:2005 | Heyman et Threlfall [15] | Ivorra et al. [16] | Lemmens et Rijnks [17] | Casciati et Al-Saleh [5] | |
| Masse du système "cloche + joug" | $m$ | $M$ | $M$ | $m$ | $M$ |
| Inertie par rapport au centre de gravité | $\Js $ | $M k^{2}$ | - | - | - |
| Inertie par rapport à l'axe de rotation | $\Js + M s^{2}$ | $M (l^{2}+k^{2})$ | - | $I_{0}$ | $I_{y}$ |
| Distance entre centre de gravité et axe de rotation ("unbalance" en anglais) | $s$ | $l$ | $a$ | $s$ | $L$ |
| Coefficient de forme | $c$ | $c$ | - | - | - |
| Gravité | $g$ | $g$ | $g$ | $g$ | $g$ |
Table 1: Notations suivant les auteurs
4 Le poids des cloches
Chaque fondeur ayant son propre tracé, et le plan de ce tracé étant un secret bien gardé, une question se pose d'entrée : est-il possible d'estimer le poids d'une cloche sans disposer du plan du tracé ? Une première solution permet de contourner le problème si on ne désire connaître que le poids (sans les poussées). Il existe des tableaux de poids, qui indiquent pour un fondeur donné le poids des cloches suivant le diamètre et l'épaisseur de la cloche. L'épaisseur de la cloche n'est que rarement exprimée numériquement sur ces tableaux. Ils font référence à des cloches de profil léger, moyen, lourd... Si un tel tableau est disponible, et que le fondeur est connu, il est alors possible de déterminer le poids de la cloche à partir d'un de ces tableaux. Cependant le même type de question va bientôt se reposer à propos de l'inertie : est-il possible de l'estimer sans disposer du plan du tracé de la cloche ? Dans ce cas il n'existe pas à notre connaissance de tableaux indiquant l'inertie des cloches. Si la cloche a une forme gothique, nous proposons alors d'utiliser d'utiliser la méthode de construction du tracé fournie par Diderot et d'Alembert [8]2. La description de l'Encyclopédie donne le tracé d'une cloche en fonction de son diamètre. Elle peut être adaptée suivant l'épaisseur recherchée pour la cloche. Notre méthode consiste à construire le plan d'une cloche type correspondant à la cloche étudiée. Ce plan est numérisé et découpé en éléments de volume infinitésimaux, dont l'intégration permet d'obtenir le volume (et donc le poids) et l'inertie de la cloche correspondante. Les justifications de cette démarche sont les suivantes :- le tracé d'une cloche permet d'obtenir un accord entre le son fondamental et la tierce, la quinte, l'octave... Il n'est pas possible de modifier la géométrie de la cloche sans modifier la hauteur des notes et ainsi désaccorder la cloche. Les différences entre les différents tracés gothiques de chaque fondeur sont donc des petites variations autour d'un tracé moyen dont il n'est pas possible de s'écarter3. Nous utilisons donc le tracé de Diderot et d'Alembert, en faisant l'hypothèse (raisonnable) que ce tracé est proche de la cloche étudiée, du point de vue du calcul de la masse et de l'inertie de la cloche ;
- les calculs conduit avec cette méthode ont montré un bon accord avec les tableaux des masses des cloches dont nous avons connaissance à ce jour (voir ci-dessous).
Fig 3: Extrait de la planche "Fonte des cloches, échantillons et diapasons" de l'Encyclopédie
Source Wikicommons
Nous avons appliqué cette méthode pour des cloches d'épaisseur $\d/\t $=11 (~ profil lourd) et $\d/\t $=15 (~ profil léger). Les résultats de ces calculs sont donnés sur le graphique suivant, où on peut lire le poids4 de la cloche en fonction de son diamètre (traits épais). Afin valider la méthode, nous avons reporté également sur ce graphique les poids5 des cloches correspondant à plusieurs fondeurs français (croix sur les graphique). On peut voir que les poids donnés par les fondeurs sont compris entre les deux situations extrêmes calculés avec la cloche type de l'encyclopédie. Ce travail de comparaison doit être poursuivit en comparant d'avantages de cloches françaises avec les résultat types. Il pourra être nécessaire de considérer des rapports $\d/\t $ plus petits que $\d/\t $=11 et plus grands que $\d/\t $=15 au fur et à mesure de l'obtention de nouveaux tableaux.
Source Wikicommons
Fig 4: Poids des cloches en fonction de leur diamètre.
Les valeurs du graphique sont à multiplier par la masse volumique en kg.m−3
Si la cloche est très ancienne et a un tracé qui n'est pas assimilable à un tracé gothique, le tracé de cloche tiré de l'Encyclopédie ne convient plus. Deux situations peuvent se présenter. Dans le meilleur des cas, un plan du tracé de la cloche existe. Il est alors possible d'effectuer les calculs décrits ci-dessus à partir du relevé. Sinon, il n'est pas possible de réaliser de calcul, puisqu'on ne connaît pas la géométrie de la cloche. Heyman et Threlfall [15] ont mis au point une technique expérimentale ingénieuse pour déterminer alors les poussées d'une cloche existante lorsqu'on ne dispose pas de suffisamment d'informations sur son tracé (voir infra).
Les facteurs suivants peuvent avoir une influence sur le poids de la cloche et ainsi créer un décalage entre le poids réel de la cloche, et celui calculé à partir de la cloche type de l'Encyclopédie :
Les valeurs du graphique sont à multiplier par la masse volumique en kg.m−3
- la géométrie de l'onde (renfort entre cerveau et anses), qui peut varier suivant les fondeurs et le type de volée (lancé-franc, retro-lancé etc.), car elle n'a pas de grande influence sur l'acoustique ;
- la géométrie des anses, même remarque que pour l'onde ;
- le procédé d'accordage, où le fondeur enlève de la masse sur la face intérieure de la cloche pour accorder cette dernière. Lors de l'accordage, une épaisseur comprise entre 0,1mm et 0,5mm est enlevée6. Le procédé d'accordage a donc une influence, mais cette dernière est faible devant les autres incertitudes régnant le poids total de la cloche (pax exemple considérer l'incertitude sur la masse volumique du métal). A titre d'exemple, le retrait de 0,5mm à une cloche de diamètre 1,00m et de profil $\d/\t $=15 conduit à une diminution de 1,2% de la masse de la cloche.
5 L'inertie des cloches
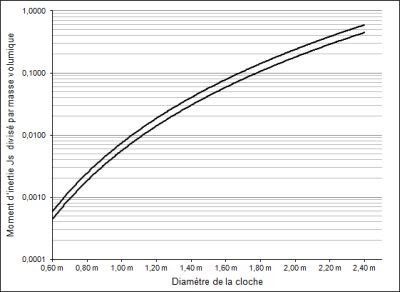
La même méthode que précédemment permet de calculer la position du centre de gravité et l'inertie par rapport à ce centre. Le centre de gravité est situé à environ 0,30$\d $ du bas de la cloche. On en déduit immédiatement la distance $s$ entre le centre de gravité et l'axe de rotation, qui apparaît dans l'équation du mouvement (1). Cette distance ne dépend presque pas du rapport $\d/\t $ (influence de l'ordre de 1%), ce qui est compréhensible car le passage d'une cloche de profil léger à lourd suit presque une homothétie. Le calcul de l'inertie $\Js $ de la cloche est peut-être la partie la plus pénible du calcul de poussée, car c'est également la partie la moins documentée. Bien que plus simple que la résolution des intégrales elliptiques d'un point de vue théorique, la difficulté à trouver des informations sur les tracés rend en pratique cette détermination laborieuse. En appliquant la même méthode que celle décrite pour le poids des cloches, on trouve l'inertie en fonction du diamètre comme indiqué sur le graphique ci-dessous, pour $\d/\t $=11 (~ profil lourd) et $\d/\t $=15 (~ profil léger).Fig 5: Inertie des cloches par rapport à leur centre de gravité, en fonction de leur diamètre.
Les valeurs du graphique sont à multiplier par la masse volumique en kg.m−3
De même que pour le poids, certains facteurs peuvent avoir une influence sur l'inertie de la cloche et expliquer un écart avec la cloche type de l'Encyclopédie :
Les valeurs du graphique sont à multiplier par la masse volumique en kg.m−3
- géométrie de l'onde (renfort entre cerveau et anses), qui peut varier suivant les fondeurs, car elle n'a pas de grande influence sur l'acoustique. Cette partie de la cloche est la plus proche de l'axe de rotation en lancé-franc. Donc l'inertie de cette partie est petite devant l'inertie du reste de la cloche, et par conséquent les variations de géométrie de cette partie ont une influence négligeable sur l'inertie calculée ;
- géométrie des anses, même remarque que pour l'onde ;
- procédé d'accordage (voir les ci-dessus). Le procédé d'accordage a une influence, mais cette dernière est faible devant les autres incertitudes régnant l'inertie totale de la cloche. A titre d'exemple, le retrait de 0,5mm à une cloche de diamètre 1,00m et de profil $\d/\t $=15 conduit à une diminution de 0,8% de l'inertie $\Js $ de la cloche.
6 Les poussées horizontales et verticales
On appelle poussées horizontales et verticales les forces qui s'appliquent sur l'axe de rotation et qui sont générées par le mouvement de la cloche. Nous avons montré que le calcul de la masse, de l'inertie et de $s$ permettent de calculer $\phi(t)$, le mouvement de la cloche en fonction du temps. Une fois cette fonction connue, les poussées horizontales et verticales peuvent être calculées à tout instant t, à l'aide des équations ci-dessous. Ces équations sont présentées dans la littérature sous des formes diverses par Ivorra et al. [16] (en fonction de $\phi(t)$ et de ses dérivées), Casciati et Al-Saleh [5] (en fonction de $\phi(t)$ uniquement) : \begin{align} H = M s \left(\phip^{2} \sin\phi - \phipp \cos\phi\right)\\ V = -M g - M s \left(\phip^{2} \cos\phi + \phipp \sin\phi\right)\\ H = M s \omega^{2} \sin \phi \left\{\cos\phi + 4\left[k^{2}-\sin^{2}(\phi/2)\right]\right\}\\ V = -M g - M s \omega^{2} \left\{-\sin^{2} \phi + 4\left[k^{2}-\sin^{2}(\phi/2)\right]\cos\phi\right\}%Caciati \end{align} avec $k = \sin \phimax $ et $\phimax $ étant le déplacement angulaire maximal de la cloche, également appelé angle de volée maximal, et $\omega = \sqrt{m g s/(\Js + m s^{2})}$. Les résultats sont données pour un exemple ci-dessous.Fig 6: Déplacement angulaire, poussée verticale (dont poids propre), poussée horizontale, en fonction du temps
Les valeurs des poussées sont rapportées à la masse de la cloche
Les valeurs des poussées sont rapportées à la masse de la cloche
7 La méthode de Heyman et Threlfall
Si le tracé de la cloche n'est pas connu, il existe cependant une autre méthode plus expérimentale pour déterminer les poussées. En 1976, Heyman et Threlfall [15] ont décrit une technique pour déduire les poussées d'une cloche à partir de deux tests simples. Le premier test consiste à mesurer la fréquence de la cloche en petites oscillations. Le second test consiste à mesurer le déplacement angulaire statique de la cloche lorsqu'on applique un moment à l'axe de rotation (par exemple en suspendant une masse sur la roue d'entraînement du mécanisme de volée). Avec cette méthode, il n'est pas possible de déterminer la masse, l'inertie du système ou la distance entre l'axe de rotation et le centre de gravité, car on ne dispose que de deux équations (fournies par les deux tests) et il y a trois inconnues. Cependant ces deux équations sont suffisantes pour en déduire les poussées, après la réécriture des formules des poussées en fonction des deux valeurs numériques déterminées lors des tests.8 Vérification expérimentale
Si on met de côté les incertitudes qui peuvent régner sur les paramètres du modèle de la cloche utilisé pour les calculs et que nous avons abordé plus haut (incertitudes sur la valeur de la masse, de l'inertie etc.), il reste à s'assurer que le modèle choisi pour représenter la cloche (pendule pesant composé) permet effectivement de retrouver le mouvement réel de la cloche. Les études expérimentales montrent un petit écart entre les résultats théoriques et les résultats mesurés. Cet écart est lié au mouvement forcé de la cloche (apport d'énergie) pour compenser les frottements (perte d'énergie). Il se traduit par une fréquence du mouvement calculée un peu plus haute que la fréquence réelle. En revanche, les enregistrements des mouvements des cloches confirment que le battant n'a qu'un effet très localisé temporellement sur le mouvement de la cloche. Beconcini et al.[3] proposent d'ajouter une petite masse ponctuelle à la cloche (additional mass model) à un endroit choisi de manière à égaliser la période mesurée (qui est facilement mesurable) avec la période théorique. Cette méthode donne de bons résultats dans l'article présenté par ces auteurs. Il est toutefois difficile de distinguer l'importance des incertitudes d'une part, et du modèle du pendule pesant composé d'autre part, sur l'écart entre mesures et résultats théoriques. Il est possible que la méthode de la masse additionnelle corrige en fait en grande partie les incertitudes sur la masse et l'inertie.9 Lexique
Il existe peu de littérature en langue française7 concernant la détermination des poussées des cloches. La grande majorité des articles sont écrits en anglais ou en allemand. Le lecteur trouvera ci-dessous quelques termes de vocabulaire utiles pour comprendre ces textes, dont celui de Heyman et Threlfall.| Anglais | Français | Allemand |
| angular displacement | déplacement angulaire | |
| axis of rotation | axe de rotation | Drehachse |
| bell | cloche | Glocke |
| bell diameter | diamètre de la cloche | Glockendurchmesser |
| bell frame | beffroi | Glockentragwek |
| bell tower | clocher | Glockenturm |
| centre of gravity | centre de gravité | Schwerpunkt |
| clapper | battant | Klöppel |
| compound pendulum | pendule pesant composé | |
| copper | cuivre | Kupfer |
| inertial form factor | coefficient de forme | Forbeiwert |
| moment of inertia | moment d'inertie | Massenträgheitsmoment |
| oscillation, swing | oscillation | Schwingung |
| swing angle | angle de volée (maximum) | Läutewinkel |
| tin | étain | Zinn |
| yoke | mouton | Joch |
| axe parallèle à l'axe de rotation et passant par le centre de gravité | Schwerachse |
10 Conclusion
Nous avons vu qu'il était possible de calculer le poids d'une cloche, son centre de gravité, et son inertie par rapport à son centre de gravité à partir de la description du tracé d'une cloche de forme gothique donnée dans l'Encyclopédie de Diderot et d'Alembert. De ces valeurs se déduisent facilement les grandeurs entrant dans le calcul du mouvement des cloches, puis leur poussée horizontale et verticale en fonction du temps. Cet article sera mis à jour progressivement lorsque nous réunirons de nouvelles informations, afin d'affiner la comparaison de notre méthode avec les valeurs qui sont fournies par les fondeurs pour les masses des cloches. L'intérêt principal de la méthode que nous proposons réside dans la détermination de l'inertie des cloches, qui est une donnée essentielle pour le calcul des poussées, mais sur laquelle il existe peu d'informations, en particulier pour les cloches existantes lorsque les fonderies d'origine ont disparu.Article mis en ligne le : 26/05/2012.
Révisé le : 02/09/2012.
Bibliographie
- [1]
- N. ANDRé : Méthodologie d'analyse mécanique des structures bois du patrimoine - Application à la réhabilitation d'un beffroi. Thèse de doctorat, Université Bordeaux I, Bordeaux, 2003.
- [2]
- P. BARRé et L. BARRé : Memento de l'architecte et de l'entrepreneur. Théorie pratique et législation du bâtiment. E. Bernard, Paris, 1896.
- [3]
- M. L. BECONCINI, S. BENNATI et W. SALVATORE : Structural characterisation of a medieval bell tower: First historical, experimental and numerical investigations. In Proc. 3rd International Seminar in Historical Constructions, Guimarães, 2001.
- [4]
- A. BELéNDEZ, C. PASCUAL, D. MéNDEZ, T. BELéNDEZ et C. NEIPP : Exact solution for the nonlinear pendulum. Revista Brasileira de Ensino de Fisica, 29(4): 645–648, 2007.
- [5]
- S. CASCIATI et R. AL-SALEH : Dynamic behavior of a masonry civic belfry under operational conditions. Acta Mechanica, 215: 211-224, juin 2010.
- [6]
- A. COINTE, P. CASTéRA, P. MORLIER et P. GALIMARD : Diagnosis and monitoring of timber buildings of cultural heritage. Structural Safety, 29(4): 337-348, oct. 2007.
- [7]
- Y. DEFORGE : Le graphisme technique : son histoire et son enseignement. Editions Champ Vallon, 1981.
- [8]
- D. DIDEROT et J. D'ALEMBERT : Cloche. Encyclopédie, ou Dictionnaire raisonné des sciences, des arts et des métiers, 1753.
- [9]
- V. DUSEIGNE : La cloche de Saint-Pierre de belleville. Tchorski - Patrimoine campanaire, cloches et clochers. http://tchorski.morkitu.org/1/belleville.htm.
- [10]
- V. DUSEIGNE : Le son d'une cloche (ch1). Tchorski - Patrimoine campanaire, cloches et clochers. http://tchorski.morkitu.org/1/son-cloche.htm.
- [11]
- V. DUSEIGNE : Le son d'une cloche (ch2). Tchorski - Patrimoine campanaire, cloches et clochers. http://tchorski.morkitu.org/1/son-cloche-2.htm.
- [12]
- H. J. GNEHM et F. HOFFMANN : Aide-mémoire de l'Office fédéral de la protection de la population, protection des biens culturels. Rap. tech., avr. 2003.
- [13]
- T. GONON : Les cloches en France au Moyen-Age : archéologie d'un instrument singulier. Hespérides. Editions Errance, mars 2010.
- [14]
- H. GOURIOU : L'art campanaire en Occident : histoire, facture et esthétique des cloches de volée. les Éd. du Cerf, Paris, 2006.
- [15]
- J. HEYMAN et B. THRELFALL : Inertia forces due to bell-ringing. International Journal of Mechanical Sciences, 18(4): 161-164, avr. 1976.
- [16]
- S. IVORRA, M. J. PALOMO, G. VERDú et A. ZASSO : Dynamic forces produced by swinging bells. Meccanica, 41: 47-62, fév. 2006.
- [17]
- K. LEMMENS et H. RIJNKS : Mathematical model for the bell SWI : project old church delft. 2004.
- [18]
- G. MENEGHETTI et B. ROSSI : An analytical model based on lumped parameters for the dynamic analysis of church bells. Engineering Structures, 32(10): 3363-3376, 2010.
- [19]
- A. PATRON-SOLARES, C. CREMONA, C. BOTTINEAU, R. LECONTE et F. GOEPFER : Study of bell swinging induced vibrations of bell tower of Metz cathedral (France). In Actes des journées scientifiques du LCPC, p. 529-536, 2005.
- [20]
- A. RUPP : Ringing Bells-State of the art in the durability evaluation of church bells. In Proceedings of the colloquium development evaluation, vol. 3, p. 29-40, Ljubljana, Slovénie, mars 2006.